Harmonic-percussive source separation¶
This notebook illustrates how to separate an audio signal into its harmonic and percussive components.
We’ll compare the original median-filtering based approach of Fitzgerald, 2010 and its margin-based extension due to Dreidger, Mueller and Disch, 2014.
from __future__ import print_function
import numpy as np
import matplotlib.pyplot as plt
import librosa
import librosa.display
Load the example clip.
y, sr = librosa.load('audio/Karissa_Hobbs_-_09_-_Lets_Go_Fishin.mp3', offset=40, duration=10)
Compute the short-time Fourier transform of y
D = librosa.stft(y)
Decompose D into harmonic and percussive components
\(D = D_\text{harmonic} + D_\text{percussive}\)
D_harmonic, D_percussive = librosa.decompose.hpss(D)
We can plot the two components along with the original spectrogram
# Pre-compute a global reference power from the input spectrum
rp = np.max(np.abs(D))
plt.figure(figsize=(12, 8))
plt.subplot(3, 1, 1)
librosa.display.specshow(librosa.amplitude_to_db(D, ref=rp), y_axis='log')
plt.colorbar()
plt.title('Full spectrogram')
plt.subplot(3, 1, 2)
librosa.display.specshow(librosa.amplitude_to_db(D_harmonic, ref=rp), y_axis='log')
plt.colorbar()
plt.title('Harmonic spectrogram')
plt.subplot(3, 1, 3)
librosa.display.specshow(librosa.amplitude_to_db(D_percussive, ref=rp), y_axis='log', x_axis='time')
plt.colorbar()
plt.title('Percussive spectrogram')
plt.tight_layout()
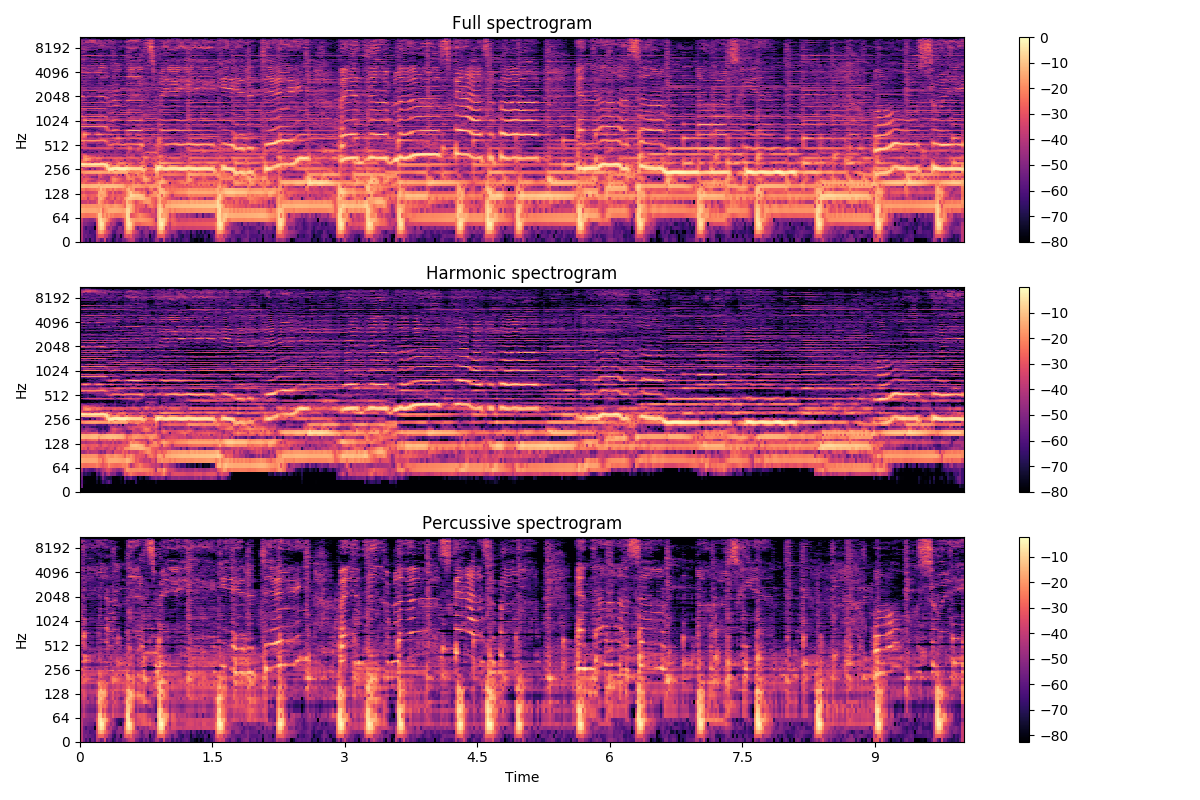
The default HPSS above assigns energy to each time-frequency bin according to whether a horizontal (harmonic) or vertical (percussive) filter responds higher at that position.
This assumes that all energy belongs to either a harmonic or percussive source, but does not handle “noise” well. Noise energy ends up getting spread between D_harmonic and D_percussive.
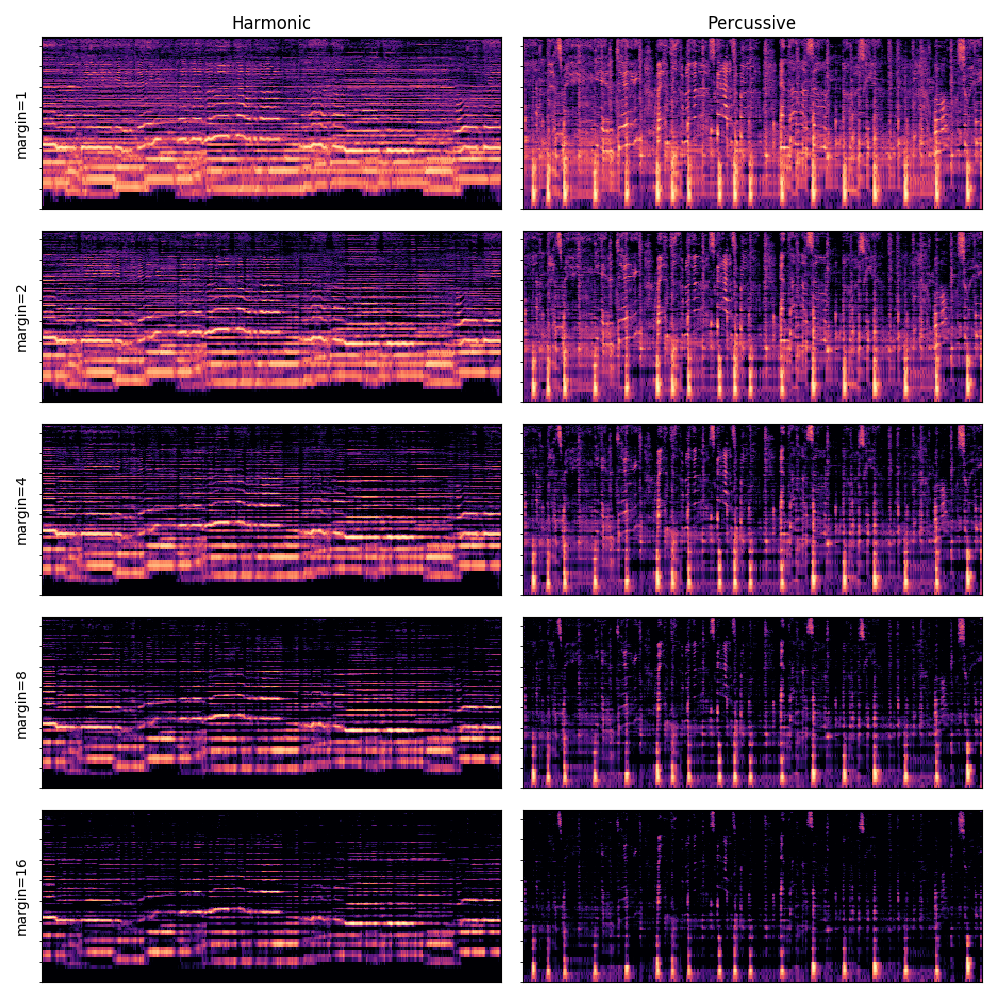
If we instead require that the horizontal filter responds more than the vertical filter by at least some margin, and vice versa, then noise can be removed from both components.
Note: the default (above) corresponds to margin=1
# Let's compute separations for a few different margins and compare the results below
D_harmonic2, D_percussive2 = librosa.decompose.hpss(D, margin=2)
D_harmonic4, D_percussive4 = librosa.decompose.hpss(D, margin=4)
D_harmonic8, D_percussive8 = librosa.decompose.hpss(D, margin=8)
D_harmonic16, D_percussive16 = librosa.decompose.hpss(D, margin=16)
In the plots below, note that vibrato has been suppressed from the harmonic components, and vocals have been suppressed in the percussive components.
plt.figure(figsize=(10, 10))
plt.subplot(5, 2, 1)
librosa.display.specshow(librosa.amplitude_to_db(D_harmonic, ref=rp), y_axis='log')
plt.title('Harmonic')
plt.yticks([])
plt.ylabel('margin=1')
plt.subplot(5, 2, 2)
librosa.display.specshow(librosa.amplitude_to_db(D_percussive, ref=rp), y_axis='log')
plt.title('Percussive')
plt.yticks([]), plt.ylabel('')
plt.subplot(5, 2, 3)
librosa.display.specshow(librosa.amplitude_to_db(D_harmonic2, ref=rp), y_axis='log')
plt.yticks([])
plt.ylabel('margin=2')
plt.subplot(5, 2, 4)
librosa.display.specshow(librosa.amplitude_to_db(D_percussive2, ref=rp), y_axis='log')
plt.yticks([]) ,plt.ylabel('')
plt.subplot(5, 2, 5)
librosa.display.specshow(librosa.amplitude_to_db(D_harmonic4, ref=rp), y_axis='log')
plt.yticks([])
plt.ylabel('margin=4')
plt.subplot(5, 2, 6)
librosa.display.specshow(librosa.amplitude_to_db(D_percussive4, ref=rp), y_axis='log')
plt.yticks([]), plt.ylabel('')
plt.subplot(5, 2, 7)
librosa.display.specshow(librosa.amplitude_to_db(D_harmonic8, ref=rp), y_axis='log')
plt.yticks([])
plt.ylabel('margin=8')
plt.subplot(5, 2, 8)
librosa.display.specshow(librosa.amplitude_to_db(D_percussive8, ref=rp), y_axis='log')
plt.yticks([]), plt.ylabel('')
plt.subplot(5, 2, 9)
librosa.display.specshow(librosa.amplitude_to_db(D_harmonic16, ref=rp), y_axis='log')
plt.yticks([])
plt.ylabel('margin=16')
plt.subplot(5, 2, 10)
librosa.display.specshow(librosa.amplitude_to_db(D_percussive16, ref=rp), y_axis='log')
plt.yticks([]), plt.ylabel('')
plt.tight_layout()
plt.show()
Total running time of the script: ( 0 minutes 4.695 seconds)