Enhanced chroma¶
This notebook demonstrates a variety of techniques for enhancing chroma features.
Beyond the default parameter settings of librosa’s chroma functions, we apply the following enhancements:
- Over-sampling the frequency axis to reduce sensitivity to tuning deviations
- Harmonic-percussive-residual source separation to eliminate transients.
- Nearest-neighbor smoothing to eliminate passing tones and sparse noise. This is inspired by the recurrence-based smoothing technique of Cho and Bello, 2011.
- Local median filtering to suppress remaining discontinuities.
# Code source: Brian McFee
# License: ISC
# sphinx_gallery_thumbnail_number = 6
from __future__ import print_function
import numpy as np
import scipy
import matplotlib.pyplot as plt
import librosa
import librosa.display
We’ll use a track that has harmonic, melodic, and percussive elements
y, sr = librosa.load('audio/Karissa_Hobbs_-_09_-_Lets_Go_Fishin.mp3')
First, let’s plot the original chroma
chroma_orig = librosa.feature.chroma_cqt(y=y, sr=sr)
# For display purposes, let's zoom in on a 15-second chunk from the middle of the song
idx = [slice(None), slice(*list(librosa.time_to_frames([45, 60])))]
# And for comparison, we'll show the CQT matrix as well.
C = np.abs(librosa.cqt(y=y, sr=sr, bins_per_octave=12*3, n_bins=7*12*3))
plt.figure(figsize=(12, 4))
plt.subplot(2, 1, 1)
librosa.display.specshow(librosa.amplitude_to_db(C, ref=np.max)[idx],
y_axis='cqt_note', bins_per_octave=12*3)
plt.colorbar()
plt.subplot(2, 1, 2)
librosa.display.specshow(chroma_orig[idx], y_axis='chroma')
plt.colorbar()
plt.ylabel('Original')
plt.tight_layout()
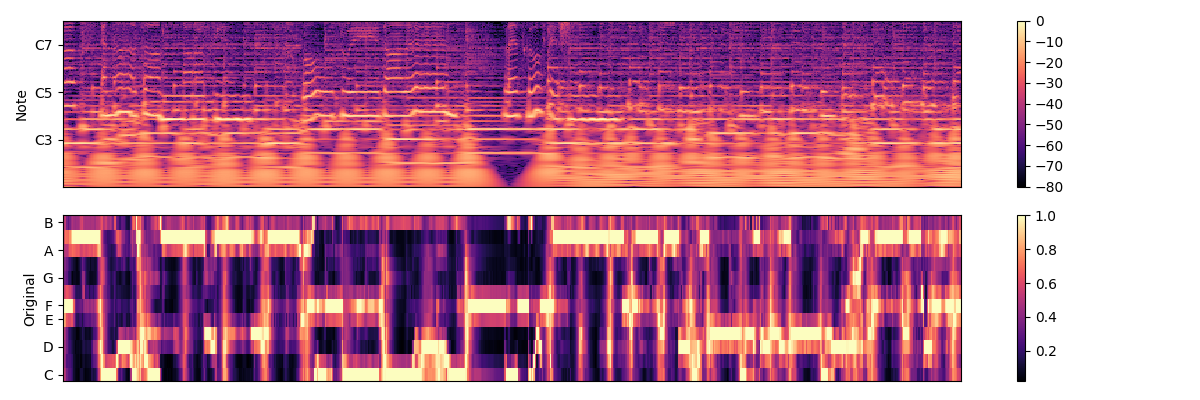
We can correct for minor tuning deviations by using 3 CQT bins per semi-tone, instead of one
chroma_os = librosa.feature.chroma_cqt(y=y, sr=sr, bins_per_octave=12*3)
plt.figure(figsize=(12, 4))
plt.subplot(2, 1, 1)
librosa.display.specshow(chroma_orig[idx], y_axis='chroma')
plt.colorbar()
plt.ylabel('Original')
plt.subplot(2, 1, 2)
librosa.display.specshow(chroma_os[idx], y_axis='chroma', x_axis='time')
plt.colorbar()
plt.ylabel('3x-over')
plt.tight_layout()
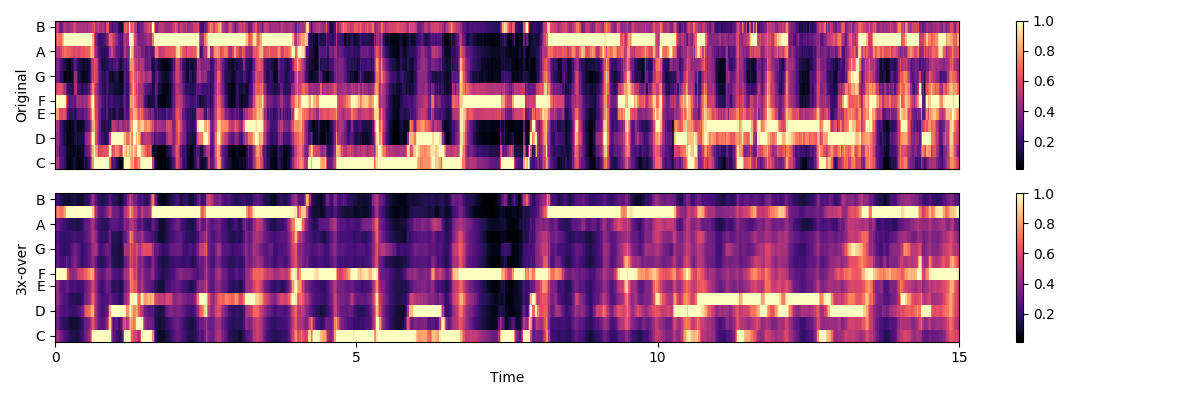
That cleaned up some rough edges, but we can do better by isolating the harmonic component. We’ll use a large margin for separating harmonics from percussives
y_harm = librosa.effects.harmonic(y=y, margin=8)
chroma_os_harm = librosa.feature.chroma_cqt(y=y_harm, sr=sr, bins_per_octave=12*3)
plt.figure(figsize=(12, 4))
plt.subplot(2, 1, 1)
librosa.display.specshow(chroma_os[idx], y_axis='chroma')
plt.colorbar()
plt.ylabel('3x-over')
plt.subplot(2, 1, 2)
librosa.display.specshow(chroma_os_harm[idx], y_axis='chroma', x_axis='time')
plt.colorbar()
plt.ylabel('Harmonic')
plt.tight_layout()
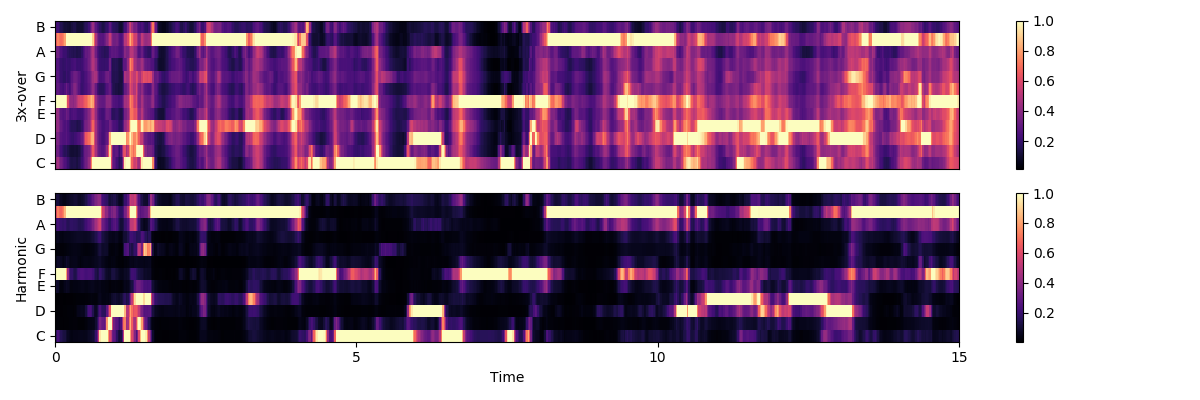
There’s still some noise in there though. We can clean it up using non-local filtering. This effectively removes any sparse additive noise from the features.
chroma_filter = np.minimum(chroma_os_harm,
librosa.decompose.nn_filter(chroma_os_harm,
aggregate=np.median,
metric='cosine'))
plt.figure(figsize=(12, 4))
plt.subplot(2, 1, 1)
librosa.display.specshow(chroma_os_harm[idx], y_axis='chroma')
plt.colorbar()
plt.ylabel('Harmonic')
plt.subplot(2, 1, 2)
librosa.display.specshow(chroma_filter[idx], y_axis='chroma', x_axis='time')
plt.colorbar()
plt.ylabel('Non-local')
plt.tight_layout()
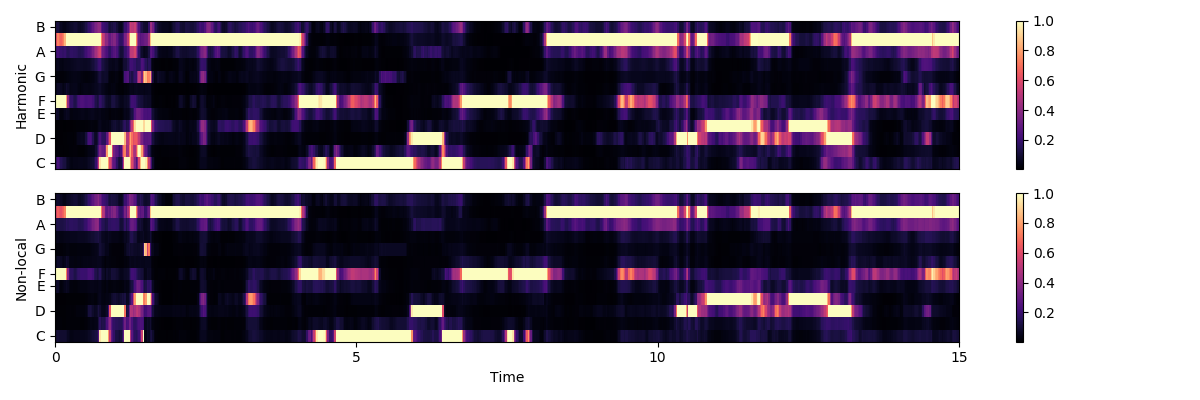
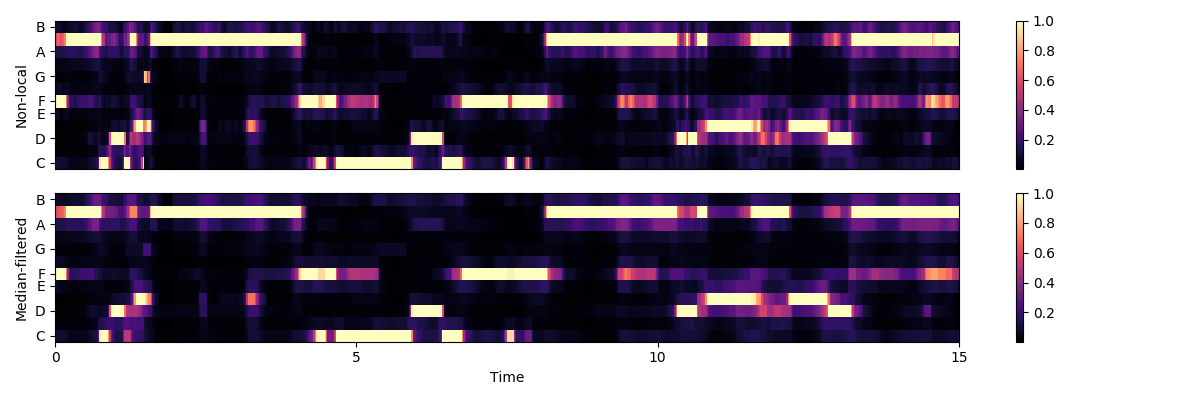
Local discontinuities and transients can be suppressed by using a horizontal median filter.
chroma_smooth = scipy.ndimage.median_filter(chroma_filter, size=(1, 9))
plt.figure(figsize=(12, 4))
plt.subplot(2, 1, 1)
librosa.display.specshow(chroma_filter[idx], y_axis='chroma')
plt.colorbar()
plt.ylabel('Non-local')
plt.subplot(2, 1, 2)
librosa.display.specshow(chroma_smooth[idx], y_axis='chroma', x_axis='time')
plt.colorbar()
plt.ylabel('Median-filtered')
plt.tight_layout()
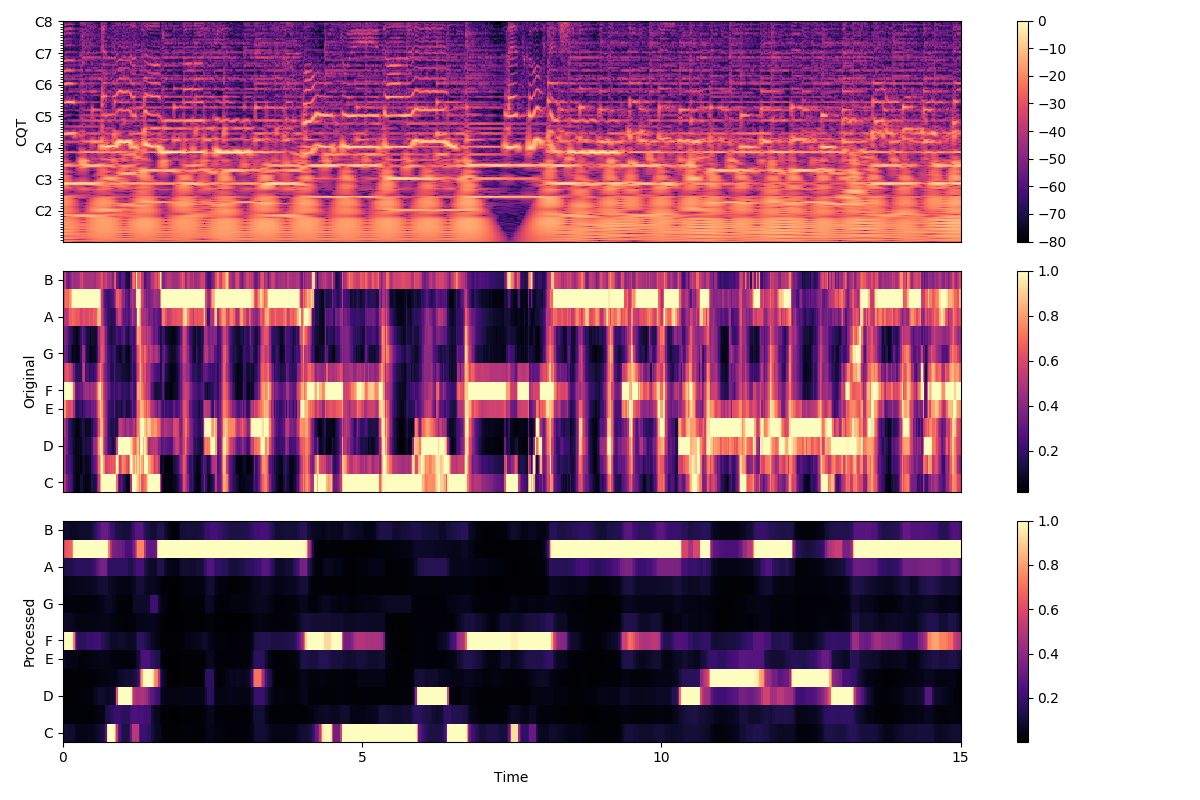
A final comparison between the CQT, original chromagram and the result of our filtering.
plt.figure(figsize=(12, 8))
plt.subplot(3, 1, 1)
librosa.display.specshow(librosa.amplitude_to_db(C, ref=np.max)[idx],
y_axis='cqt_note', bins_per_octave=12*3)
plt.colorbar()
plt.ylabel('CQT')
plt.subplot(3, 1, 2)
librosa.display.specshow(chroma_orig[idx], y_axis='chroma')
plt.ylabel('Original')
plt.colorbar()
plt.subplot(3, 1, 3)
librosa.display.specshow(chroma_smooth[idx], y_axis='chroma', x_axis='time')
plt.ylabel('Processed')
plt.colorbar()
plt.tight_layout()
plt.show()
Total running time of the script: ( 0 minutes 26.508 seconds)